什么是跳表?
跳表是平衡树的一种替代方案,可实现Log(n)级别的插入、删除。和平衡树不同的是,跳表并不保证严格的“平衡性”,而是采用更为随性的方法:随机平衡算法。
下面来研究一下跳表的核心思想:
先从链表开始,如果是一个简单的链表,那么我们知道在链表中查找一个元素I的话,需要将整个链表遍历一次。

如果是说链表是排序的,并且节点中还存储了指向前面第二个节点的指针的话,那么在查找一个节点时,仅仅需要遍历N/2个节点即可。

这基本上就是跳表的核心思想,其实也是一种通过“空间来换取时间”的一个算法,通过在每个节点中增加了向前的指针,从而提升查找的效率。
如何构建跳表
按照上面生成链表的方式,上面每一层链表的节点个数,是下面一层的节点个数的一半,这样查找过程就非常类似于一个二分查找,使得查找的时间复杂度可以降低到O(log n)。但是,这种方法在插入数据的时候有很大的问题。新插入一个节点之后,就会打乱上下相邻两层链表上节点个数严格的2:1的对应关系。如果要维持这种对应关系,就必须把新插入的节点后面的所有节点(也包括新插入的节点)重新进行调整,这会让时间复杂度重新蜕化成O(n)。删除数据也有同样的问题。
为了避免这一问题,skiplist不要求上下相邻两层链表之间的节点个数有严格的对应关系,而是为每个节点随机出一个层数(level)。比如,一个节点随机出的层数是3,那么就把它链入到第1层到第3层这三层链表中。为了表达清楚,下图展示了如何通过一步步的插入操作从而形成一个skiplist的过程: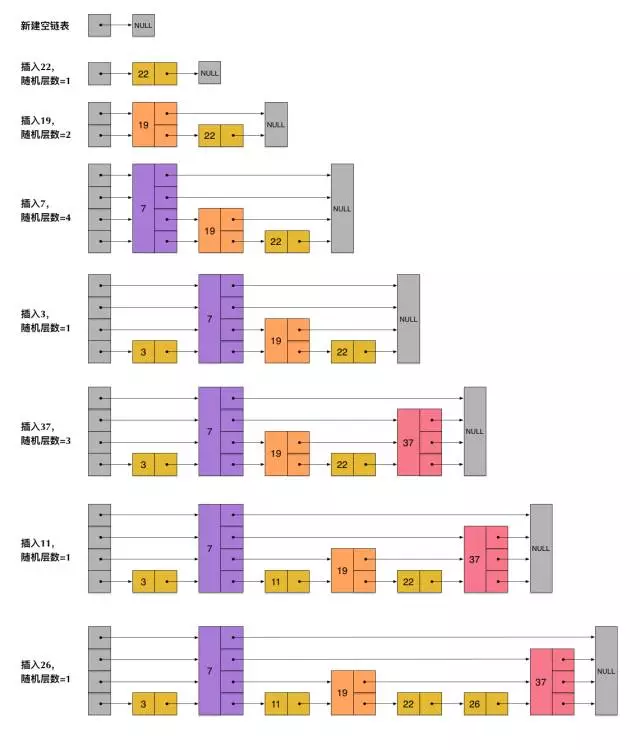
如何确定层数?
节点插入时随机出一个层数,仅仅依靠这样一个简单的随机数操作而构建出来的多层链表结构,能保证它有一个良好的查找性能吗?因此并不是一个普通的服从均匀分布的随机数,它的计算过程如下:
- 首先,每个节点肯定都有第1层指针(每个节点都在第1层链表里)。
- 如果一个节点有第i层(i>=1)指针(即节点已经在第1层到第i层链表中),那么它有第(i+1)层指针的概率为p。
- 节点最大的层数不允许超过一个最大值,记为MaxLevel。
这个计算随机层数的伪码如下所示:
randomLevel()
level := 1
// random()返回一个[0...1)的随机数
while random() < p and level < MaxLevel do
level := level + 1
return levelrandomLevel()的伪码中包含两个参数,一个是p,一个是MaxLevel。在Redis的skiplist实现中,这两个参数的取值为:
p = 1/4
MaxLevel = 32根据前面randomLevel()的伪码,我们很容易看出,产生越高的节点层数,概率越低,无论如何层数总是满足幂次定律(power law,越大的数出现的概率越小)。定量的分析如下:
- 节点层数至少为1。而大于1的节点层数,满足一个概率分布。
- 节点层数恰好等于1的概率为1-p。
- 节点层数大于等于2的概率为p,而节点层数恰好等于2的概率为p(1-p)。
- …
因此,一个节点的平均层数(也即包含的平均指针数目),计算如下: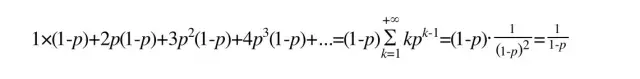
很容易计算出:
当p=1/2时,每个节点所包含的平均指针数目为2;
当p=1/4时,每个节点所包含的平均指针数目为1.33。(Redis skiplis的空间开销)
如何查询?
由于跳表数据结构整体上是有序的,所以查找过程就是一个在上下层之间,在同一层中不断由前向后比对的过程。刚刚创建的这个skiplist总共包含4层链表,现在假设我们在它里面依然查找23,下图给出了查找路径: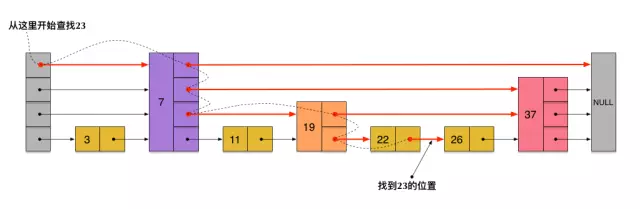
如何插入删除?
以在插入时,需要首先查找到合适的位置,然后就是修改指针(和链表中操作类似),然后更新跳表的level变量。由于同时要更改若干层的指针,跳表使用一个update数组来辅助指针切换。在查找的过程中,一旦当前节点的后继节点为空,或者后继结点比插入节点要大,说明找到了插入节点在该层的前驱节点,记录到update数组中。在切换指针时只需要遍历update数组即可完成所有层的指针切换。下图给出了插入路径,红色部分即为update数组内容。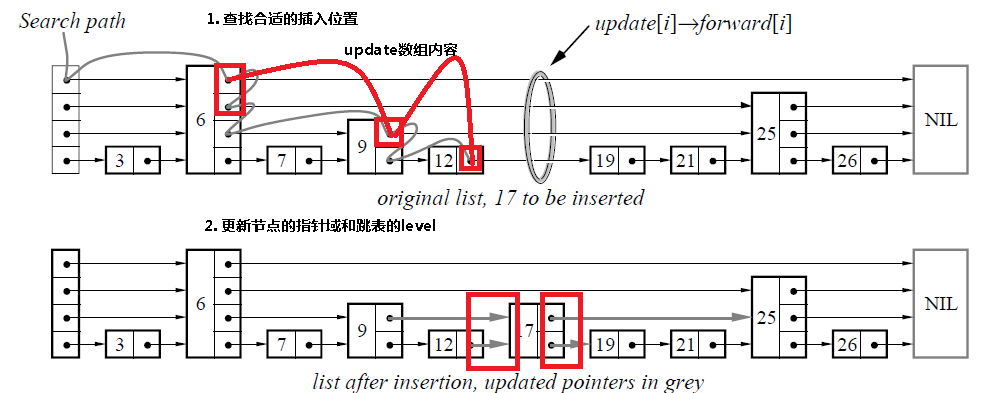
Redis为什么用skiplist而不用平衡树?
Redis的作者 @antirez 是怎么说的:
There are a few reasons:
- They are not very memory intensive. It’s up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.
- A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.
- They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.
来源链接:https://news.ycombinator.com/item?id=1171423
本文作者 : cyningsun
本文地址 : https://www.cyningsun.com/06-18-2018/skiplist.html
版权声明 :本博客所有文章除特别声明外,均采用 CC BY-NC-ND 3.0 CN 许可协议。转载请注明出处!
