描述
字符串匹配查找常见的算法或数据结构有:暴力搜索、KMP算法(Extend-KMP、BM算法、Sunday算法)、AC自动机、前缀树(Double Array Trie)、后缀树(后缀数组)。以下汇总它们的算法比较,以及关键点: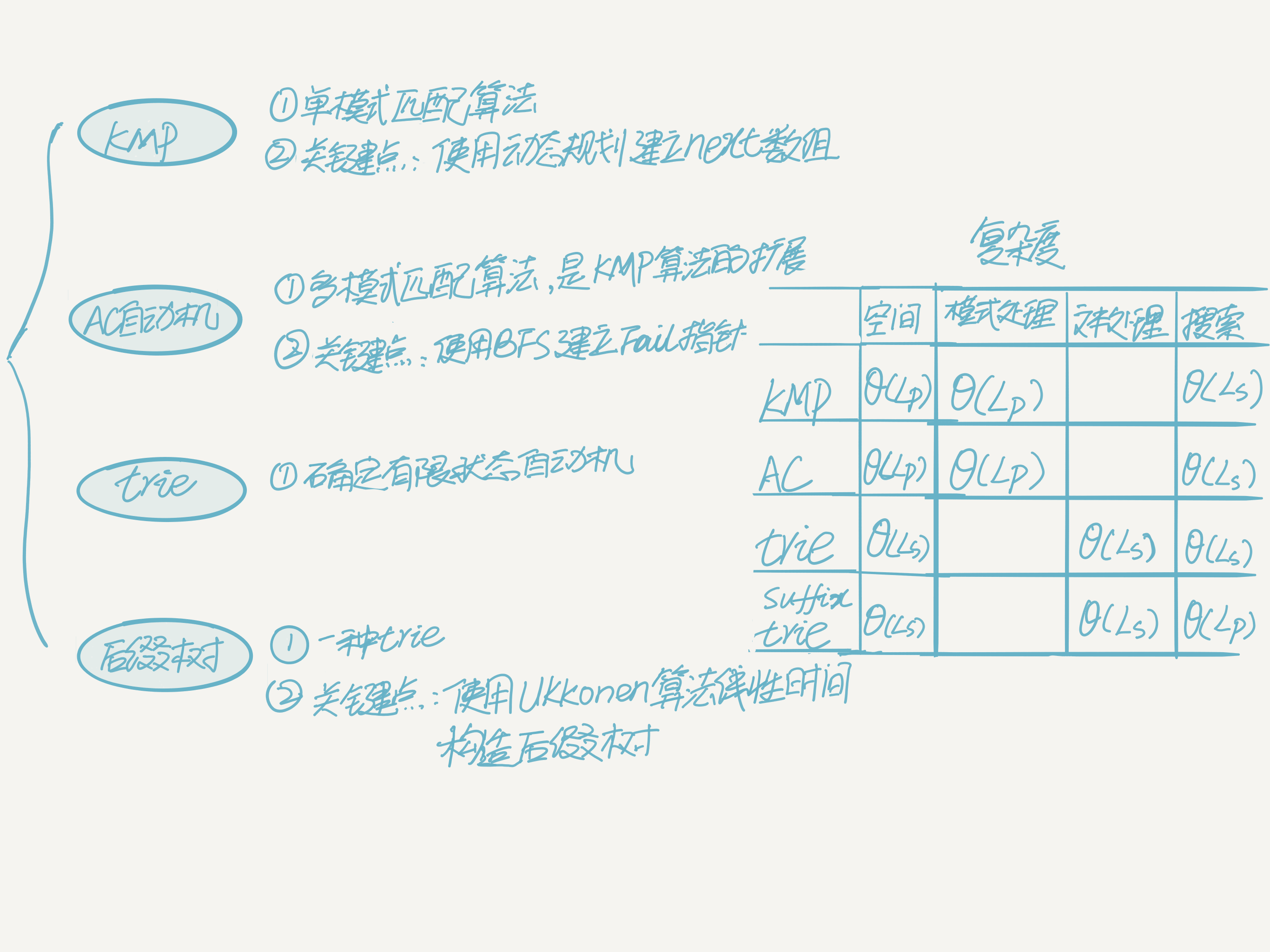
关键点描述
KMP算法
模式串需要移动的距离=模式串已匹配的字符长度-(模式串已匹配字符串)前缀后缀最长公长度
next数组(前缀后缀最长公长度)求解:N为next数组,i为数组位置,P为模式串
- 1、当i=0,N[0]=0
- 2、当i=1,如果P[1]=P[0],N[1]=N[0]+1;否则N[1]=N[0]
- 3、当i=j,如果P[j]=P[N[j-1]],N[j]=N[j-1]+1;
否则,i=N[j-1],如果i>0,重复上述计算,否则,N[j]=0
AC自动机
- 1、为模式串建立Trie(标志模式串的节点特殊标记,用于匹配时确认匹配成功)
- 2、为Trie建立Fail(失败)指针(在匹配路径上失败的时,跳转到合适的位置进行下次匹配)
- 3、对字符串进行匹配(遍历Trie,进行匹配)
Fail指针的建立:对于一个节点C,标识字符a,顺着C的父亲节点的失配指针走,走到第一个有儿子也是a的节点D,那么C的失配指针就指向D的标识a的儿子节点(假设为E,从根节点到E节点表示的模式串P2是从根节点到C节点的字符串的后缀P1的后缀,当模式串P1匹配失败时,尝试匹配模式串P2,这是Fail 指针的本质作用)。如果找不到这个节点,那么失配指针指向Root
Ukkonen后缀树算法
活动节点:是用于查找一个后缀是否已经存在这棵树里,即查找的时候从活动节点的子节点开始查找,同时当需要插入边的时候也是插入到该节点下;
活动边:是每次需要进行分割的边,即成为活动边就意味着需要被分割;而 活动长度 则是指明从活动边的哪个位置开始分割。
剩余后缀数:是我们需要插入的后缀的数量,说明程序员点就是缓存的数量,因为每次如果要插入的后缀存在,则缓存起来。
活动点(active point) :三元组(活动节点,活动边,活动长度)
后缀连接:如果一个步骤插入(Insert)两个以上新的节点,如果该新节点不是当前步骤中创建的第一个节点,则将先前插入的节点与该新节点通过一个特殊的指针连接,称为后缀连接(Suffix Link)。后缀连接通过一条虚线来表示,连接由前一个节点指向后一个节点。从根节点到达后缀连接指向节点的字符串,是从根节点到达后缀连接源节点的字符串的后缀。所以后缀连接的前一个节点需要分割时,需要同时分割后缀连接指向的节点。
代码实现
(未完待续)
参考文档
后缀树: http://www.cnblogs.com/gaochundong/p/suffix_tree.html
Ukkonen 的后缀树算法的清晰解释: http://www.oschina.net/translate/ukkonens-suffix-tree-algorithm-in-plain-english
Aho-Corasick自动机浅析: https://segmentfault.com/a/1190000000484127
AC自动机算法: http://m.blog.csdn.net/article/details?id=7002823
从头到尾彻底理解KMP算法: http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
从头到尾彻底理解KMP算法: http://blog.csdn.net/v_july_v/article/details/7041827
本文作者 : cyningsun
本文地址 : https://www.cyningsun.com/04-10-2016/string-match.html
版权声明 :本博客所有文章除特别声明外,均采用 CC BY-NC-ND 3.0 CN 许可协议。转载请注明出处!
